For simplicity, below I assume L1 has full access to the Computation Dag structure, and can calculate the corresponding scopes of all VProgs. I will not concern myself much with how this is done. This assumption might eventually be relaxed using an enshrined L2, or just pushing the issue to each L2 individually.
Pruning in Kaspa consists of throwing away transaction data. If a transaction scope requires executing transaction data from below the pruning point, it could fail or succeed depending on the real time performance of the node, and it is clear such a transaction should not be allowed. I will argue below that the effects of disallowing this on the functionality are non crucial:
For a potential transaction x, let W_x denote the set of vertices created by x, let F_x denote the set of witnesses provided to the Prog_v, and let P_x denote all the paths from W_x to a vertex in F_x. Finally, let Y denote the set of vertices which are currently proven.
Observation: let C\subseteq Y be a covering of all paths in P_x. Then there is an equivalent transaction x’ creating the same set of vertices W_x, which provides the witnesses C instead, and introduces a scope of computation contained in the one originally introduced in X.
Remark: there is no guarantee that the number of witnesses (i.e. the size of C) provided by x’ will be smaller than in x, and it in fact can be bigger. As a sidenote, it may be beneficial on general to determine heuristics to find a set which does reasonably well for both the “width” of the cut and the scope size.
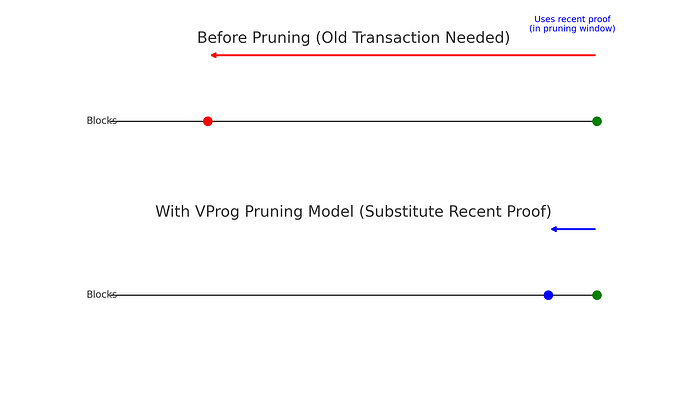
The above observation implies that in order to obtain the same functionality as a transaction x, one can equivalently provide witnesses for “later” vertices, so that the scope will be contained within the pruning period. This however requires these later vertices to be “proven”, but all this requires is that a recent proof of the corresponding account exists up to this pruning period. It is a reasonable requirement to expect that VProgs aiming to be composed with recent proofs, will provide proofs within the latest pruning period. It is remarked that under our design, a prover can always prove old data even after an extended period of inactivity (see On the design of based ZK rollups over Kaspa's UTXO-based DAG consensus)
Correspondingly, the data of a vertex in the computation Dag lying below the pruning point can be discarded. Pruning of the Dag structure is ignored for now, but as an afterthought we could prune it as well and only store membership proofs of its pre-pruned structure.
Discarding long-proven account data
While the above limits the number of vertices data need to be stored, storing intermediary states for the entire pruning period remains a big load. For this reason we should also introduce regular pruning of vertices lying far below a recent zk proof.
Specifically, extend the definition of a vertex to (a,t,T), with the last entry denoting at which block number the transaction was accepted, i.e. its “round”.
Let then v=(a,t,T) be a vertex, and \pi_a be the latest proof submitted for the account a, then v shouldbe discarded when T<T’-\Delta (\Delta=500 for example) where T’ denotes the “round” of the latest transaction proven by \pi_a.
This scheme is logical because:
a) The more time surpasses following it, the less likely it is a vertex will need to be read.
b) if such a vertex absolutely must be read, witnesses for it could still be provided for it via the intermediary states commitment on \pi_a. I.e. the functionality remains possible, but merely requires including witnesses again.
There is a case for including another condition - that if a vertex was recently read, it will not be discarded for \Gamma (=50) rounds. Logic being that sometimes transaction scopes will be rebuilt in parts, hence reerasing them immediately will be detrimental. This however further complicates the objective inferring of a transaction scope.
*The numbers 50, 500 etc. are pure placeholders.