This post was deeply inspired by ideas shared with me by @hashdag, @michaelsutton, and @proof. It assumes a strong foundational understanding of ZK concepts and the workings of ZK-protocols. This blog post is far from being a detailed design proposal, but the core concept is accurately outlined.
A previous post by @michaelsutton outlined the basic L1<–>L2 interaction. Here I dive in further into the technical bits:
- About Proving System Choice for L1 zk verification
- L1 Enhancements / Additions
a. Low level elliptic curve opcodes
b. L1 zk-verify function pseudo code as it should be implemented in Kaspa script
c. ZK-friendly hash function choice (partly finished, require separate blogpost)
d. UTXO ( input / output ) Anchoring via KIP10 (so-called canonical bridge) - Possible L2 design examples
a. Single proving system
b. zkVM base solution
c. Pseudocode for zk-SNARK Verification for Groth16
Additionally, the general guideline for implementing L2 solutions on top of Kaspa L1 should prioritize minimizing L1 modifications, ensuring support for a wide range of L2 solutions, and maintaining a strong guarantee of bounded performance impact for zk-verification executed by L1 nodes.
This post serves as an attempt and example of how zk-L2s can be supported with minimal changes to the BTC-like Kaspa script language and L1 architecture, while still offering flexibility for diverse implementation options.
Terminology and concepts adopted from @michaelsutton post:
- Recursive DAG ordering commitments Merkle root
- State UTXO / State commitment UTXO
- L1 based rollups (zk)
- ZK-related opcodes (OpZkVerify)
1. About Proving System Choice for L1 zk verification
Groth16 / Plonk proving systems are proposed to be utilized due to their small proof size and constant-time verification complexity, which are critical for maintaining L1 performance.
Groth16/ Plonk proving systems are highly stable, with thoroughly debugged technology stacks and rigorously audited, well-established mathematics. Despite not being recent developments, they remain state-of-the-art in terms of proof size, verifier efficiency, and overall stability and security. Moreover, these proving systems are the only ones natively supported by major blockchain networks such as Ethereum.
Proving System zk-stacks & stability: Codebases for zk-proving systems like Groth16 and Plonk are mature, extensively tested, and battle-hardened across various blockchain ecosystems. This reduces the risk of bugs or implementation errors, ensuring a stable and secure integration.
Elliptic Curve Choice: Groth16 / Plonk zk-proving systems are based on the BN254 elliptic curve (a Barreto-Naehrig curve with a 254-bit prime field). While these systems can operate with other pairing-friendly elliptic curves, BN254 offers a security level of approximately 100 bits, which is considered sufficient for many practical applications. Additionally, it is already supported by Ethereum-like chains, making it a strong candidate for adoption.
2. L1 Enhancements / Additions:
To enable zk-proof verification and interaction between L1 and L2, the following enhancements are proposed:
2.a. Low level EC operations:
Additions to BTC like Kaspa-script language:
- ADD: Modular addition for elliptic curve field arithmetic.
- MUL: Modular multiplication for elliptic curve field arithmetic and scalar multiplications.
- PAIRING: Executes elliptic curve pairing operations, required for verifying Groth16 / Plonk proofs.
Source of Opcode Implementations:
- Implementations for `ADD`, `MUL`, and `PAIRING` opcodes will be derived from the stable and widely adopted blockchains, such as Ethereum. Most stable implementations are zCash, Geth (and maybe reth)
- Ethereum’s opcode implementations for BN254 are well-tested and optimized for performance, providing a reliable foundation.
2.b. Details about Groth16 / Plonk ZK-Verify-Function (executed by L1 nodes):
The verify function will be implemented directly in terms of the BTC-like Kaspa scripting language, along with the verification key and state hash. The exact definition of public parameters can vary based on the application, but this design ensures flexibility and trustless execution across use cases.
The verification process requires only two public inputs *** enabling support for practically any desired logic. The verify function can be defined with four arguments:
- Verification Key: Less than 1kB.
- Public Parameter 1: 256-bit.
- Public Parameter 2: 256-bit.
- zk-Proof: Less than 1kB.
The verification itself involves dozens of elliptic curve (EC) operations (ADD, MUL, and PAIR) and can be efficiently implemented within a Bitcoin-like Kaspa script if these operations are supported as was proposed earlier in this post.
*** In general, more than two public inputs can be supported; however, the number should always be bounded, as the verification complexity increases linearly with the size of the public inputs.
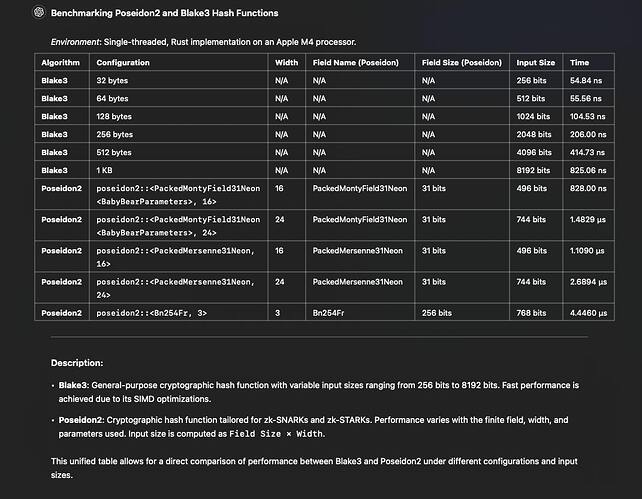
2.c. ZK-friendly hash function choice (partly finished, require separate blogpost)
L1 must provide additional support for zk-based L2 systems to prove transaction ordering as observed by L1. This ensures consistency and enables verifiable state updates. zk-L2s will leverage Merkle Inclusion Proofs, using Merkle Roots computed by L1 to verify transaction inclusion and ordering without requiring direct access to the complete transaction history during L1 verification.
L1 will construct a Merkle Tree, where each leaf corresponds to an individual transaction. The Merkle Root will represent the set of all transactions in a block, and will be computed by L1 with a zk-friendly hash function (e.g., Poseidon2, Blake2s, or Blake3) ensuring compatibility with zk systems. This structure is referred to as Recursive DAG ordering commitments in a previous post by @michaelsutton
Hash Function Considerations
- Efficiency: L1 requires a highly efficient hash function optimized for standard CPUs, as it must be executed by all Kaspa nodes.
- zk-Friendliness: L2 requires zk-friendly hash functions to compute inclusion proofs for each L2 transaction during proof generation.
- Security: The selected hash function must ensure robust security across both L1 and L2.
For example, while the Blake2s/Blake3 family of hashes is field-agnostic and suitable for L1 (cpu friendly), it is significantly less performant than zk-friendly options like Poseidon2, which offers better compatibility with zk-proofs but is finate field dependent. Blake2s / Blake3 zk performance currently about at least 20 times slower than this of Poseidon2, moreover major zkVMs should be extended with Blake hash as its precompile circuit that is not a big problem but still should be done accurately and properly audited ( which can delay mainnet L2s )
Most major zkVMs (such as SP1, CairoVM, Risc0, Jolt, and Nexus) would / should be compatible with the proposed choice of hash function. “Compatible” means prove generation performance or number of circuit constraints per hash per byte of hashed data etc …
An alternative approach could involve selecting a hash function optimized for Groth16 / Plonk, but this comes with at least two significant drawbacks:
- Fixed Tree Size: Groth16 and Plonk require a fixed tree size. While this limitation is manageable, it imposes a strict proving interval, meaning the number of transactions in the tree must remain constant for single zk-proof.
- Performance Impact: A more critical issue arises because transaction order and inclusion would not be proven by the zkVM itself. Instead, these transactions would become public inputs for the second-stage proving system (i.e., the zkVM verifier implemented using Groth16/Plonk). This approach results in increased zk-proof generation times, negatively impacting performance.
The relationship between hash function choice, cpu vs zk performance and the dependency on finite field will be explored in a future blog post.
Sub-Nets Support
To enhance scalability and parallel processing, transactions can be categorized into sub-nets. The Merkle Tree’s leftmost leaf will store the Merkle Root of the previous block and its merge-set (all transactions), ensuring consistent chain linkage.
2.d. UTXO ( input / output ) Anchoring via KIP10 (so-called canonical bridge)
By utilizing KIP10 introspection opcodes, UTXO-input and UTXO-output anchoring can be incorporated into the spending script. This mechanism enables any party to provide a valid zk-proof to spend a State UTXO, ensuring that the newly created UTXO complies fully with the rules defined by the L2 state transition logic. It guarantees verifiability and security of L2 state transitions in a fully trustless manner, as KIP10 enforces the creation of specific UTXO-outputs when spending UTXO-inputs.
This topic will be explored in greater detail in a separate blog post. For now, it suffices to say that KIP10 facilitates the linking of UTXO-inputs and UTXO-outputs within the same transaction through commitments.
Summary for L1 additions:
- Math OpCodes: ADD, MUL, PAIR - allow implementation of zk-verifier (aka OpZkVerify)
- Merkle-Tree structure with zk-friendly hash function - allow TX inclusion proofs and ordering during state transaction (open question: hash function choice)
- Open Question: A dedicated opcode for constructing a Merkle root from public inputs may be required—this will be addressed separately. In any case, the aim is to minimize additions to L1. The current Bitcoin-like Kaspa script capabilities are sufficient to support basic hash composition of public inputs. However, for more advanced schemes, L1 may need to provide additional support in the future.
3. Possible L2 Implementation examples
How to Store L2 State in L1 UTXO
The ScriptPubKey will store a hash representing a specific verification function, including its verification key and the L2 state hash. Zk-proof public parameters act as commitments to the previous and next states, dag recursive commitments and output UTXO (and maybe input UTXO), ensuring that the spending process is fully trustless.
The ScriptPubKey field in L1 UTXOs will store the following information related to L2 state:
- Recursive DAG ordering commitments Merkle root
- State-Hash: Represents the Merkle root of the L2 state
- Program-Hash: Specifies the zk-circuit or state transition program.
- Verification-Key: Enables zk-proof verification on L1
- ZK-Verification code
3.a. Example of a Single zk-proof system:
State transition programs can be implemented directly using Groth16 or Plonk proving systems. This approach is well-suited for smaller, predefined, or existing solutions, for example zCash ZK core is implemented in terms of this proving system and at least theoretically can be deployed as is.
In such cases, a single zk-proof is generated and verified on-chain.
3.b Example of a zkVM based solution:
Another potential implementation for L2 is a zkVM-generated proof of state transitions. A zkVM enables the efficient execution of arbitrary smart contracts or virtual machine code (e.g., EVM, SVM) with state transitions verified through zk-proofs. This approach ensures program correctness while maintaining efficiency in proof generation and verification.
Leveraging zkVM technology offers significant development flexibility and numerous essential features. Currently, zkVMs represent the dominant approach in the industry. They are continually improving, becoming more user- and developer-friendly, as well as increasingly efficient. Furthermore, two-stage proving can be seamlessly extended to N-stage proving, as zkVMs are capable of supporting additional zk-schema implementations on top of their existing framework.
zkVM Codebase Compatibility: This approach enables integration with major zkVM codebases, including Risc0, SP1, and CairoVM and others, ensuring broad interoperability and ecosystem growth.
Example of using 2 zk-proof systems (zkVM→Groth16/Plonk):
- zkVM (e.g., Risc0, CairoVM, SP1): This system will prove the execution of a state transition program (e.g., EVM) alongside transaction ordering and inclusion proofs.
- Groth16 / Plonk: This proving system will implement a zk-verifier for the zkVM. zkVM proof will be feeded inside Groth16 / Plonk circuit that implement zkVM verifier. This will generate another zk-proof that going to be verified on-chain by L1. It will generate a zk-proof that is sent on-chain and verified by all Kaspa L1 nodes.
3.c. Pseudocode for zk-SNARK Verification for Groth16.
Constants
- PRIME_Q (256 bits, 32 bytes): Prime field size for alt_bn128 (aka BN254) elliptic curve.
Data Structures
1. G1Point (512 bits, 64 bytes) - Represents a point on the curve with:
- x (256 bits, 32 bytes).
- y (256 bits, 32 bytes).
2. G2Point (1024 bits, 128 bytes):
- Represents a point on the extension field with:
- x[0], x[1] (each 256 bits, 32 bytes).
- y[0], y[1] (each 256 bits, 32 bytes).
3. VerifyingKey (640 bytes):
- alfa1 (G1Point, 64 bytes).
- beta2 (G2Point, 128 bytes).
- gamma2 (G2Point, 128 bytes).
- delta2 (G2Point, 128 bytes).
- ic (array of G1Points, size depends on the number of public inputs + 1; each G1Point = 64 bytes).
4. SnarkProof (192 bytes):
- a (G1Point, 64 bytes).
- b (G2Point, 128 bytes).
- c (G1Point, 64 bytes).
Elliptic Curve Math
1. P1 and P2:
- P1 (512 bits, 64 bytes): Generator point for G1.
- P2 (1024 bits, 128 bytes): Generator point for G2.
2. Negate Point:
- Input: G1Point (64 bytes).
- Output: Negated G1Point (64 bytes).
3. Addition:
- Inputs: Two G1Point values (each 64 bytes).
- Output: Resultant G1Point (64 bytes).
4. Scalar Multiplication:
- Inputs: G1Point (64 bytes), scalar s (256 bits, 32 bytes).
- Output: Scaled G1Point (64 bytes).
5. Pairing:
- Inputs: Arrays of G1Point and G2Point (each G1Point = 64 bytes, each G2Point = 128 bytes).
- Output: Boolean (1 byte).
6. Pairing Check:
- Input: Four pairs of G1Point and G2Point (4 x 64 bytes + 4 x 128 bytes = 768 bytes).
- Output: Boolean (1 byte).
Verification Logic (logic that will be supported directly by L1)
1. Verify Function:
- Inputs:
- vk (Verification Key, 640 bytes).
- input (Array of public inputs, each 256 bits, 32 bytes; total size = number of inputs × 32 bytes).
- proof (SNARK proof, 192 bytes).
- Steps:
1. Input Validation:
- Ensure input.length + 1 == vk.ic.length.
- Ensure all input[i] values are less than FIELD_SIZE (256 bits, 32 bytes).
2. Compute vk_x:
- Start with vk_x as G1Point (0, 0) (64 bytes).
- For each public input:
- Scale vk.ic[i + 1] (64 bytes) by input[i] (32 bytes) using scalar_mul.
- Add the result to vk_x (64 bytes) using addition.
- Add vk.ic[0] (64 bytes) to finalize vk_x.
3. Pairing Check:
- Use pairingProd4 (extended pairing function for 4 arguments) to verify the pairing:
- Inputs: Negated proof a (64 bytes), proof b (128 bytes), vk.alfa1 (64 bytes), vk.beta2 (128 bytes), vk_x (64 bytes), vk.gamma2 (128 bytes), proof c (64 bytes), and vk.delta2 (128 bytes).
- Output: Boolean (1 byte).
- Output:
- Returns true (1 byte) if the proof is valid, false (1 byte) otherwise.
Summary of Sizes
1. Key Sizes:
- Verification Key: 640 bytes. (example for 2 public inputs)
- Public Inputs: Each 256 bits, 32 bytes.
- SNARK Proof: 192 bytes.
2. Operations:
- Addition (G1Point): Input = 64 bytes × 2, Output = 64 bytes.
- Scalar Multiplication (G1Point): Input = 64 bytes + 32 bytes, Output = 64 bytes.
- Pairing Check: Input = 768 bytes, Output = 1 byte.